There is a board with 2 rows and N columns, represented by a matrix M. Rows are numbered from 0 to 1 from top to bottom and columns are numbered from 0 to N−1 from left to right. Each cell contains either a 0 or a 1. You know that:
- the sum of integers in the 0-th (upper) row is equal to U,
- the sum of integers in the 1-st (lower) row is equal to L,
- the sum of integers in the K-th column is equal to C[K].
Your job is to recover M based on this information.
Write a function:
function solution(U, L, C);
that, given two integers U, L and an array C of N integers, as described above, returns a string describing the matrix M in the following format. The first part of the string should be the description of the upper row (N characters: 0 or 1), then there should be comma (,), and finally there should be the description of the lower row (N characters: 0 or 1.) The output string should not contain any whitespace.
If there exist multiple valid Ms, your function may return any one of them. If no valid M exists, your function should return the word IMPOSSIBLE.
Examples:
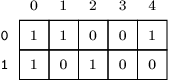
1. Given U = 3, L = 2, C = [2, 1, 1, 0, 1], your function may, for example, return 11001,10100 which describes the following board:
2. Given U = 2, L = 3, C = [0, 0, 1, 1, 2], your function should return the word IMPOSSIBLE, because no matrix M satisfies such conditions.
3. Given U = 2, L = 2, C = [2, 0, 2, 0], your function should return 1010,1010, which describes the following board:

Write an efficient algorithm for the following assumptions:
- U and L are integers within the range [0..100,000];
- N is an integer within the range [1..100,000];
- each element of array C is an integer within the range [0..2].